More than 25 years after the fall of communism in East-Central Europe, the subject of its economic transition from a centrally administered economy to a free-market configuration has begun to shift from the research agenda of economics or the political and social sciences to the agenda of the discipline of history with all of its various facets.[1] The sociological, economical and politological research that began immediately after 1989/90 has already produced a huge amount of works illuminating the reshuffling of institutions, rules and practices, changes in economic output and the changing structure of local industries and societies.[2] In recent years, however, there has been growing interest on the part of historians seeking to explore several other aspects of the post-communist transition.[3] Various phenomena such as the politics and culture of memory, the return of strong nationalist narratives in the post-communist societies or the immediate history of the political upheavals of 1989/90 have been taken into account.[4] The economic transition has also attracted some attention with respect to the intellectual history of economic thought,[5] the shattering social consensus of late socialist societies,[6] the personal continuities beyond the 1989/90 rupture[7] and the symbols and narratives of particular anti-communist upheavals.[8] Recently, Philipp Ther presented a synthetic narrative of ›the New Order on the Old Continent‹, i.e. of the neoliberal wave that swept large – and especially the Eastern – parts of Europe after 1989/90.[9]
The following paper tries to venture into precisely this territory, i.e. to historicize the roots and outcomes of the post-1989 economic change in the particular case of Czechoslovakia. It looks at the language of the economic change that began to emerge in the late 1980s and accompanied the first critical perestroika engagements with the socialist planned economy. I will argue that certain patterns of thought and argumentation were already established within the Czechoslovak scholarly community in the late 1980s which were then quickly broadened after the collapse of state socialism and used to promote a particular version of liberal market transformation.
A similar case was made recently by Jacek Kochanowicz for the situation in Poland. Analyzing the rhetoric of the main Polish daily Gazeta Wyborcza in the immediate post-1989 period, he shows that the free-market blueprints were partly legitimized by referencing and monopolizing a distinct set of values, such as rationality and logic. When the centrally administered economic order collapsed and space opened for debate about possible economic restructuring, these values were used to frame the whole discussion and to establish an interpretative monopoly about distinct economic policies.[10]
In Czechoslovakia, I will argue, the situation was similar, but had its roots in the pre-1989 era. In the first part I will thus concentrate on the patterns of thought and argumentation that were used within the Czechoslovak scholarly community of economists that critically engaged with the official economic doctrine. I will focus on the discussion that took place in the major scholarly journal Politická Ekonomie (Political Economy), where possibilities of market reforms were discussed as early as the second half of the 1980s. Here a distinct mode of argumentation and language was established that accompanied the liberal mode of economic reform immediately after 1989. In the second part I will then follow the dissemination and changes that this particular market rhetoric underwent as a result of ›going public‹ within a newly emerging public space.
1. Defining Standards: Semantics of Czechoslovak
Reform Economics during Perestroika
As is well known, Czechoslovakia was one of the most ideologically constrained communist dictatorships in East-Central Europe throughout the 1970s and 1980s, with very rigid party control over social and cultural life. The suppression of the Prague Spring and the following purges in the so-called ›normalization‹ period struck, with enormous vigor, those academic disciplines which were considered a bedrock for reformist ideas. Here the social sciences and humanities were mistrusted the most, economics being one of the main targets of the purges. A large number of scholars were ousted from their academic positions, every paper intended for publication was placed under strict ideological censorship, university curricula for teaching economics were restructured, and translations of Western scholarship made during the 1960s were banned from teaching practice. Travel to foreign conferences was carefully monitored, as were any other contacts with foreign scholars.[11]
With the older generation cut off from the relevant academic infrastructure and networks, intellectual innovation within the field depended very much on the younger scholars. Some key works of Western economic thought that had been removed from the university lectures and libraries remained accessible in the specialized libraries of the Czechoslovak Academy of Sciences. It was therefore in these academic institutions that the circles – at first very small – of readers and students who were willing and able to keep up with developments in their field were to be found. Here the first communities of young academics were formed, mainly doctoral candidates or younger post-docs born in the 1940s and 1950s. Since the majority of them were in their early thirties or even late twenties, it is safe to say (and many of them have acknowledged this in retrospect) that it was precisely this early socialization in the professional field of scholarly economics that enabled them to frame their everyday experience with the deficits of centrally planned economy in scholarly language and then theorize about its flawed substance and possibilities for change.[12] It is therefore interesting to take a closer look at the kind of knowledge they acquired during this formative phase.
The most effective ways of keeping up with the dynamics within Western economics were either the few translations or a direct reading of Western works available in the local environment. One particular piece of economic scholarship is notable here. It stood for the most synthetic embodiment of current thought within the discipline and served as the main tool for transferring Western economic knowledge to the Czechoslovak context. Although some other texts were available and read during the 1970s and particularly 1980s, it was the textbook with the simple title Economics: An Introductory Analysis written by Paul A. Samuelson (later joined by William D. Nordhaus) in 1948 that was the main reference point for many of the young Czechoslovak economists.[13] The textbook had been rewritten and re-edited several times since its first publication, so by 1985 it was already the twelfth edition that served as the main source of information about the current state of the discipline in Western university departments.[14] For the young Czech academics, it was this particular choice of Samuelson’s textbook in its later versions that played the major role in constituting the consensus about ›proper‹ economic thinking and theory.
The choice of an economic textbook originally written for beginners as the main source of information for a scholarly community is central in this respect. Looking at the position of textbooks within economics in the 1970s and 1980s in general and at Samuelson’s text in particular, we may uncover its special function. If we take the classic distinction made by Thomas Kuhn in his Structure of Scientific Revolutions, the role of a textbook is very much determined by the field it is dealing with. While the natural science textbooks generally summarize the well-defined body of findings and theories upon which there is a clear understanding within the given scholarly community, the role of textbooks in social sciences and humanities is quite different. They stand rather for an introduction into the discipline, giving an overview of the main competing approaches and encouraging or even requiring parallel reading of primary sources, research reports and other text genres. In this way, the reader is constantly reminded of the research context and discussions beyond the textbook and thus receives a broad picture of the discipline, where there is always a variety of solutions available from which he or she is supposed to choose the one most suitable for a given problem.[15]
This was not, however, the case with Samuelson’s book. He did not conceive his text as an introduction to be supplemented by the reading of other genres of academic writing, but rather as a summary of given knowledge in economics presenting a coherent overview of the state-of-the-art consensus. This positioning of the text as the embodiment of all economic knowledge was in fact reinforced with every new edition. While the preface to the first edition from 1948 states that the textbook was written as an introduction for those who did not want or need to pursue economics beyond the basic level, the preface to the seventh edition from 1967 introduces the text as encompassing ›nothing unnecessarily hard, but nothing essentially omitted as being beyond the grasp of the serious student; and above all, nothing that later must be unlearned as wrong‹.[16]
Both ongoing and past discussions within the field were effectively downplayed more and more with each new edition, and every such edition made further steps towards presenting the textbook in the manner of the natural sciences, i.e. as a clear and uncontested body of knowledge shared by all scholars of the discipline. In fact, not only was the genre of the text moving towards this conception, but the very discipline of economics was gradually portrayed as having more in common with the natural than the social sciences, let alone the humanities. Even in the first edition published in 1948, the reader was advised that the first task of ›economic science [my italics, R.K.] is to describe, to analyze, to explain, to correlate […], to simplify, to abstract, to idealize‹. The seventh edition published in 1967 stated that ›economics uses the deductive methods of logic and geometry, and inductive methods of statistical and empirical inference‹, and the eighth edition (1970) used the notion of economics being the ›queen of social sciences‹, where its primacy was conceived as the closest to the ›exact‹ natural sciences.[17] From the very beginning of the book, the reader was directed to think about economics as about a natural science, preferably physics or chemistry. The book itself was written as a natural science textbook, giving a clear overview of the state-of-the-art knowledge with all ›invalid‹ theories and findings being rejected. No discussion took place, no questions were raised, no further readings were encouraged.
In terms of content, Samuelson, and later also Nordhaus, presented a neoclassical synthesis that sought to bring together the various strands of economic thought, postulating rationally acting individuals that try to maximize their utility, with Keynesian impulses that rehabilitated the role of state interventions, particularly on the macro level. As such, it was quite remote from the radical market agendas later proposed by the Czechoslovak reformers. But it was the professional language of Samuelson and Nordhaus that had great appeal for the Czechoslovak scholarly community. It is important to realize that the first edition of the text available was the sixth edition published in 1964, and the majority of local scholars made use of even later editions published throughout the 1970s and 1980s.[18] As a result, the impression they gained of the state-of-the-art Western type of economics was that of an exact science operating with clear methodology, well-functioning models and standards of evidence, giving accurate and unquestionable information on the problems addressed.
Although Samuelson’s textbook was not the only piece of Western scholarship available in Czechoslovakia, it was the most popular one among the younger Czech economists. The handful of other texts translated into Czech more or less reconfirmed the basic argument put forward by Samuelson. Roy G.D. Allen’s two books Mathematical Economics (translated into Czech in 1971) and Macroeconomic Theory. A Mathematical Treatment (translated in 1975) conveyed Samuelson’s main message of perhaps even more clearly.[19] Presenting mathematical methods as the only way of reaching serious findings and theories, economics was presented as a sort of ›universal social science‹ with reliable and objectively tested solutions.
The picture of scientific economics provided by these texts was in fact not unknown east of the Iron Curtain. Building upon traditions of lively contacts between Soviet and Western economists from the 1950s and 1960s, mathematical economics started to become institutionalized in the Soviet Union parallel to the Western development during the 1970s.[20] Reinvigorated by the Nobel Memorial Prize in Economic Sciences for Leonid Kantorovic and Tjalling Koopmans in 1975, it created a disciplinary culture that contributed to a distinct self-identification of younger economists, for whom the mathematical methods embodied representations of rationality and ›truth-finding‹ devices such as analytical tools, theories, etc.[21] Socialized in a very tight network of personal relations among a few dozen individuals of similar age and common reading material, the group of younger economists born in the 1940s and early 1950s acquired a very strong professional identity and was prepared to radically challenge its field as it entered the second half of the 1980s.[22]
When the onset of the Gorbachev era in the Soviet Union with the proclaimed perestroika and glasnost forced even the ideologically extremely rigid Czechoslovak leadership to recognize the worsening performance of the planned economy, the door began to open to this new generation of economists. The loosening of the hitherto very tight constraints on public and, above all, academic debate in the mid-1980s affected the field of economics in particular, where the most energy was invested and from which the most helpful outcomes were anticipated.[23] In 1986, a special Institute for Economic Forecasting was created at the Czechoslovak Academy of Sciences. It was tasked with elaborating a thorough economic analysis of the causes of the economic downturn and drafting guidelines for economic restructuring.[24] Lead by Valtr Komárek, one of the prominent economists of the generation spearheading the 1968 reform movement, the institute profited from his personal networks within the highest levels of the communist hierarchy and secured very broad political backing for its work. Komárek himself belonged to the generation of 1968 but was nevertheless able to summon a very broad spectrum of scholars, encompassing many of the younger economists socialized in the Czechoslovak Academy of Science in the 1970s and 1980s as well.[25] Provided with such an institutional safe haven, the future architects of Czechoslovak reforms such as Václav Klaus, Karel Dyba, Tomáš Ježek, Dušan Tříska, Vladimír Dlouhý and others worked in the ›grey zone‹ of late socialism, i.e. in the environment of people not opposed to, or sometimes even members of, the structures of the communist system and therefore able to keep up with the recent developments within their professional fields, but who were nevertheless neither active communists nor sympathizers with the political or ideological opposition.[26]
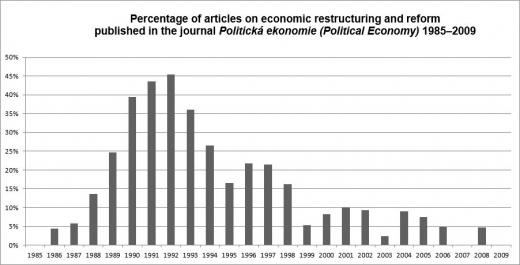
These academics were thus not banned from expert discussion and were able to take part in the perestroika debates in Czechoslovakia with tremendous vigor. In the context of the late 1980s, it was their unique language and lines of argumentation, drawing on Western canonical texts, that constituted what was arguably the most refreshing school of thought in the debates and one which very quickly found its way into major journals.[27] In this context, the journal Politická Ekonomie (Political Economy) was of enormous significance. As the oldest journal in the Czech language registered in Web of Science and by far the most central one in the field of economics, it dominated the discussion about the ›restructuring of economic mechanisms‹, i.e. the Czechoslovak version of perestroika that was officially proclaimed in 1987. Published on a monthly basis until 1991 and on a bimonthly basis thereafter, and with each issue containing about 10 to 15 articles, it amassed the respectable number of 1,066 articles from the onset of the discussion in 1986 until the breakup of Czechoslovakia at the end of 1992. Of course, not all of the articles dealt with possible changes to the economic system, but a quantitative analysis of the journal content shows very well how the importance of this topic within the field of economics evolved.
As we can see, while the debate about the possibilities of economic reform began somewhat slowly and hesitantly, it gradually gained momentum. This trend culminated in the years 1990–1994, when more than one quarter – in the years 1991–1992 almost one half – of all papers published in the journal dealt in one way or another with the subject of economic reform. An overwhelming majority of these articles were published by members of the Forecasting Institute, who effectively dominated the whole discussion when the debate began to unfold in 1987 and 1988. With Samuelson’s textbook and other similar texts as the main framework of their professional expertise, the younger generation of Klaus, Dlouhý and others started to publish increasingly critical articles reflecting their position towards the whole concept of the centrally planned economy.
One particular article deserves special attention here. The text, written by Václav Klaus and Dušan Tříska (who would become the key adviser to Klaus in his office of Czechoslovak finance minister in the early 1990s), entitled ›Economic Center, Restructuring and Equilibrium‹[28] and published in the August 1988 issue, has a reputation as the epitome of all radically critical texts. It has been quoted many times as the most comprehensive account of the problems of the late socialist economy as well as the most influential proposal for swift market reform that Czech scholarship has produced. A closer look on this paper can shed greater light on how the specific professional socialization of Czech free-market scholars shaped the form of their argument.
The notably short text of only twelve pages is introduced by a general statement that the hitherto existing discussion on the Czechoslovak economic restructuring suffered from a lack of analysis of practically everything – of the causes of the current condition, of the future direction, and of the appropriate course. Having dismissed the relevance of the current discussion, Klaus and Tříska go on to claim in the introductory passages that their text is grounded in a ›standard‹ economic theory, which is, however, neither specified nor mentioned in any of the footnotes. Indeed, the very notion of an undefined ›standard‹ is central to the entire text. The macroeconomic dimension of state intervention is treated ›in agreement with the standard economic thought‹,[29] and the criteria of efficiency deployed by the authors are labeled as ›standard‹,[30] thus creating the overall impression that the position of the authors simply reproduces an already given consensus in the Western economic community.
Following Samuelson’s reasoning, the authors see their approach as an exact one, as close as possible to physics. The message of the text is often metaphorized in the appropriate language, with frequent use of words like ›equilibrium‹, ›force field‹, etc. ›Microeconomic analysis postulates the equilibrium as an equilibrium of interacting, individually analyzed subjects, as an equilibrium of force fields generated by them‹,[31] the authors argue, expressing the idea that every economic agent has distinct interests which together should lead to the preferred state of balance.
Equipped with the ›standard‹ economic theory and a natural science vocabulary, the authors go on to identify the flaws in the existing economic setting, where the planning center mistakenly substitutes the ›standard‹ role of market consumer-producer relations.[32] Following the classic argument of Ludwig von Mises, Klaus and Tříska argue that the center can never have enough information to get the prices right, and that this can only be accomplished in an unrestricted market economy. This substantial flaw in the existing setting is, they claim, systematically underestimated both in practice and by the given theoretical scholarship and leads towards all kinds of disequilibria, which are ›in every economy, in every moment and in every economic system an economic evil‹ (emphasis by the authors).[33] On the basis of this argument they categorically refuse the existing proposals for economic reform, claiming that they lack the basic understanding that there are ›simple, universally and generally valid rules according to which the economic subjects behave‹.[34] Here the article reaches its argumentative climax and gives a clear message: According to ›standard‹ economic theory, the planned economy is by definition flawed, and any attempts at restructuring it are doomed to fail. The only way out is the acknowledgement of ›universally and generally valid rules‹ postulated and represented as in the natural sciences, which inevitably lead to a single outcome, namely the discarding of any form of state regulation and rapid introduction of a fully developed market.
In putting forward this argument, Klaus and Tříska radically departed from the existing framework of the economic reform debates of late socialism in terms of content while in fact remaining loyal to its general argumentative pattern. The emphasis they placed on market functions, especially on prices, and the complete omission of questions of income equality, clearly went beyond the socialist economic discourse. However, the basis of the argument, claiming that there were universally valid economic rules, actually reproduced the Marxist narrative about inevitable, objective patterns of economic development and human behavior.
While Klaus and Tříska were more or less using the rhetorical strategies acquired from Samuelson, the content of their argument deployed one more school of economic thought. The references to the key function of prices as the main source of information for all market participants and the energy invested in discrediting the whole concept of economic planning referred indirectly to the classic works of Ludwig von Mises and to his intellectual successors centered around Friedrich August von Hayek and other members of the ›Austrian‹ school with their fundamental skepticism regarding state activities in the economic field.
As in the case of Samuelson, the works of Hayek were far from unknown in Czechoslovakia. Though the first official translations of his works, most notably The Road to Serfdom (originally published in 1944), were not published until 1989, there was a semi-official samizdat translation made by the future Czechoslovak Minister of Privatization, Tomáš Ježek, in the late 1980s which was widely disseminated and read among Czech economists. Thus Samuelson’s form of presenting the scholarly field of economics, building upon the notion of an objective, natural-science-like discipline, merged with the radical market content of the ›Austrian‹ approach, which dominated the mode of thought of many now middle-aged Czechoslovak economists.
As some cultural economists and historians have noted, the different schools of economic thought are connected not only with specific arguments but also with specific modes of representing their reasoning. Indeed, each economic school of thought uses a distinct ›emplotment‹ to make its argument appealing to the audience. The story of Hayek’s and Friedman’s liberal paradigm is that of a romance, where the ›little man‹ fights on the side of good against the almighty state.[35] In the Austrian story in particular, entrepreneurs are the heroes and the free market is the heavenly world, whereas the state stands for the big evil to be defeated. The narrative describes the chance for everyone to succeed, if only the evil government is kept out of the way.[36]
This is in fact also the story told by Klaus and Tříska in their scholarly article. They cast the economic center and its intervention in the economy as the origin of all problems and argue that its complete disengagement would spell victory for universally valid reason, so heavily tested and tortured under the circumstances of the socialist economy. If the center is disengaged, the ›evil‹ of disequilibria disappears and the ›universal rules‹ brought to light by the ›standard‹ scientific theory ensure overall prosperity and happiness. Following the romantic plot, the good eventually prevails against all odds.
2. Implementing Standards: Semantics of Czechoslovak Economic Reform after the Fall of Communism
There are many indications that it was precisely this romantic emplotment connected with the Austrian economic paradigm that the reformers presented not only to their academic audience, but, from the end of 1990 onwards, also to the broader Czechoslovak public, and which substantially helped the particular form of economic reform to become so successful. As some historians and literary scholars have noted recently, the fall of communism in Czechoslovakia was accompanied by an essential shift of the prevailing literary plot in the public discourse. Whereas in the 1970s and 1980s many Czechs and Slovaks perceived their situation more or less in the mode of irony, stressing the absurdity of living in ›real socialism‹, the police atrocities against a peaceful student demonstration on November 17, 1989 triggered a substantial shift towards a romantic plot.[37]
At first it was the detailed descriptions of the police action against the helpless unarmed students. The TV images of students being encircled and brutally beaten by specially trained elite police forces served as the basis for the romantic narrative and contributed to the overall public mobilization against what was perceived as the ruthless rule of violence. The general mobilization against state violence, the assertion of human rights and the overall enthusiasm about dismantling the fierce dictatorship further fueled the romantic emplotment. Later on, metaphors of catharsis and rebirth made their way into the public discourse, and a ›new society‹ was anticipated as an expression of the substantial ontological change.[38]
There were initially no economists in the executive bodies of the Civic Forum as the main, dissident-dominated public initiative of the revolution, but the younger employees of the Forecasting Institute were very quick to offer their professional expertise and join the revolutionary community in November 1989.[39] All of a sudden they found themselves at the center of political decision-making and became the only group able to provide answers to the question of economic reforms.[40] As a result, Czechoslovakia never utilized foreign economic advisors to such an extent as, for example, Poland, relying instead by and large on transformation blueprints that were based on internationally shared knowledge, but produced mainly by local economists.
At the time the Civic Forum composed its first political program, the economic part was fully entrusted to the two most visible members of the Forecasting Institute group, Vladimír Dlouhý and Václav Klaus. This gave them the opportunity to introduce their theoretical knowledge, cultivated in the debates of the 1980s, into political practice. Not surprisingly, the basic ideas about the future economic setting developed more and more towards a free-market economy with a primacy of private ownership.[41] While the first political program of November 26, 1989 still mentioned that all types of ownership should be considered equal,[42] the official scenario for the economic reform drafted after the decisive election victory of the Civic Forum in June 1990 envisioned rapid privatization of a substantial part of the state sector. It also mentioned the control of inflation as the primary objective to which all other issues, including unemployment, should be subordinated.[43] Here again the motif of ›standards‹, already tested as a valid tool of reasoning in the academic discussion prior to 1989, played a pivotal role. The rapid shift towards a free-market economy where private ownership dominated was represented as a shift towards a ›standard‹ economic setting derived from the findings of the objective science of economics. ›Economic principles, just as the principles of physics, are always valid‹,[44] was a frequent justification for the reform steps taken and for the rapid implementation of the free market, which was also seen as the most effective tool for redistribution.
Particular representations of this key motif were extremely important in the first months after the start of the reforms, when the ›shock‹ experienced by broad sections of the population was most dramatic. On January 1, 1991, full price liberalization was introduced overnight. Consumer prices skyrocketed while wages were still restricted by a tight fiscal policy.[45] Small-scale privatization was launched on the same date, and in February a law was passed enabling the large-scale privatization of big enterprises. In 1991, the currency was devaluated two times and inflation rose by more than 50 percent. However, exports rose significantly in 1991, generating a surprising surplus as early as June of that year. The rise of the unemployment rate stopped at 6.6 percent in 1991 and declined to 5.1 percent in 1992, which most probably saved the government from significant social unrest and opposition.[46]
During this period of fast and deep changes, a distinct mixture of representations of economic knowledge, of ›the West‹ and of the own national history emerged, partly appropriating the fading discourse of late 1989 and early 1990. While the economic measures taken were constantly defended as being embedded in ›standard‹ scientific theory, the goal of the restructuring was cast as a ›return to Europe‹, one of the buzzwords of the 1989 events.[47] In the autumn of 1989 and the beginning of 1990, this slogan was used to capture the overall idea of overthrowing the rule of violence and one-party dictatorship and of introducing universal human rights and the basic rule of law. As was the case with all of the revolutionary slogans, claims and debates of late 1989 and early 1990, economic issues were not among the main topics addressed.[48]
However, with the gradual decline of the Civic Forum, the revolutionary community slowly began to hand over the power and initiative to newly emerging institutions. Elections took place at the beginning of June 1990, generating a legitimate parliament and government. Early in 1991, the Civic Forum, the overall platform for engaged citizens, fell apart, and from its ruins a classical spectrum of political parties without claims to universal representation began to emerge. The former unity of the revolutionary community was gone and with it the notion of a ›return to Europe‹ as a general slogan to capture the revolutionary enthusiasm. It was at this very moment that the slogan was revived and invested with new meaning in the narrower context of the economic changes. The Czech liberal right recast this ›return to Europe‹, no longer using it to signify the overthrow of communist dictatorship and subsequent adoption of democracy and human rights, but to represent the ongoing changes in the economic setting. Europe as an ›empty signifier‹ was invested with economic content, and the transformation was cast as a return to a natural state.
After the launch of the economic reform in 1991, the spatial dimension of the ›return‹ was substituted with a temporal one. With more and more voices emphasizing the varieties of capitalism in Western Europe, it was no longer possible to represent the economic reform as a mere adoption of some universal ›European‹ setting. Rather, it was cast as a ›return‹ to the indigenous Czechoslovak version of Europe, which was found in the allegedly golden age of interwar Czechoslovakia. Standing as a symbol of national sovereignty (thus reflecting the national revival following the fall of communism) and economic prosperity, it was the interwar republic which became the main positive reference point for the economic ›return to Europe‹.[49]
The picture of interwar Czechoslovakia as almost a pure antithesis to communist Czechoslovakia made it possible to represent the ongoing changes as a return to an already tested model from national history. The First Czechoslovak Republic was seen as a bedrock of prosperity and liberal economic thought. The liberal Finance Minister from the early 1920s, Alois Rašín, was repeatedly cited as an inspiration, and the allegedly successful economic performance of the First Czechoslovak Republic served as a confirmation of the chosen path of transformation.[50] Key reformers never missed an opportunity to reiterate that it was the portrait of none other than Rašín that took a prominent place in their offices.[51] The economic reform was thus cast not as an appropriation of some Western European model, but primarily as a return to the nation’s own past, itself an embodiment of the ideal liberal market setting.
While there could have been no doubt that interwar Czechoslovakia was an integral part of the European democratic tradition, there was also no problem with casting the economic reform as genuinely European. As a matter of fact, the free-market face of interwar Czechoslovakia was seen as being more ›European‹ than the Europe of the early 1990s itself. The Czechoslovak reformers scarcely missed an opportunity to emphasize the redundant state intervention into the economy in any Western European country. If there was a positive picture of the West at all, it was that of Thatcher’s Great Britain, not of Kohl’s Germany or Mitterrand’s France, and the Czechoslovak reformers repeatedly expressed their vision that the liberal market restructuring of post-communist East-Central Europe would, in the long run, bring a similar ›liberal revolution‹ all over the continent. As Václav Klaus noted in one of his popular articles published in defense of the rapid economic transformation: ›The pendulum of history swings against all kinds of socialism and etatism. It is a verified historical truth that once it comes to such a fundamental change of direction, it takes a very long time to change it back again. After centuries of laissez-faire, a trend began to dominate in the late nineteenth century that culminated not only in the communist and national-socialist experiments of the twentieth century, but also in efforts to build a Western welfare state – efforts that, despite first appearances, were no less dangerous.‹[52]
On these grounds, many oppositional voices against the rapid transition to a full market economy were easy to dismiss.[53] As already noted, the majority of reformers were not in strict opposition to the communist regime during the late 1980s, but nor were they generally active in the party structures. However, the critics of the reform blueprints, advocating more gradual reforms with greater state involvement, were mainly recruited from the older generation of scholars influenced by the experience of the Prague Spring and engaged in one way or another in the party apparatus. They were thus easily discredited either by mentioning their involvement in the pre-1989 Communist Party or by pointing out the etatist nature of their argument and labeling them ›crypto-communists‹. Suggestions coming from continental Europe, on the other hand, were easy to dismiss as something foreign and invalid for the East-Central European tradition of economic success embodied in interwar Czechoslovakia.[54]
Together with these revisions of the key slogan ›return to Europe‹, the romantic emplotment gained new dynamics as well. As the initial romantic narrative of the Velvet Revolution began to fade during the early 1990s, and with it the unity of the revolutionary community, it was replaced by the romance of the liberal economy. Medical metaphors of a miraculous recovery from a serious disease – very often cancer – dominated the discourse and were present in many speeches or newspaper articles dealing with economic reform.[55] Interviews with the leading reformers and other articles dealing with issues of economic reform in the most read Czechoslovak dailies increasingly bore titles like ›private owners as a cure‹,[56] ›healing by shock‹[57] or ›return to naturalness‹.[58] Emphasis was placed on the assumed natural condition of the Czechoslovak economy as ›healthy‹, manifested in the prosperity of interwar Czechoslovakia and firmly based on the traditionally skilled and talented Czechoslovak people, with a rejection of any kind of ›government injections‹ for the privatized enterprises. Shock therapy (though less shocking than in Poland) seemed to be the appropriate medical treatment to redirect the economy to its ›natural‹, prosperous state, so well known from the interwar period.[59]
(© Czech News Agency/ČTK – Photo 2015/Tomáš Novák)
The declared symbol of interwar Czechoslovakia made it then possible to pursue the so-called ›Czechoslovak‹ path that gave preference to the privatization of many large-scale enterprises into the hands of Czechoslovak citizens. While some of the key enterprises were indeed sold to foreign capital, the romantic concept of national renewal and revolution made it hard for the pattern of privatizing into foreign hands to be generally accepted. Apart from small enterprises that were sold in local auctions, then, large enterprises were often privatized by means of the ›voucher method‹, whereby every citizen could buy a set of coupons representing his or her share in national enterprises for a symbolic price. By investing these coupons in a maximum of ten firms or in one of the investment funds that functioned as intermediaries, a concrete number of shares was calculated and transferred into the ownership of every citizen. In this way the participation of potentially every state citizen in the creation of the new market order was to be achieved practically overnight and at minimal cost. Communist subjects were to be remade as capitalist shareholders.[60]
(© Czech News Agency/ČTK – Photo 2015/Jaroslav Hejzlar)
(Wikimedia Commons/Photo: Rios; Public Domain)
The romance of the fall of communism and the vision of a new, non-violent society were replaced by the romance of creating an economic order with maximum participation. This transformation was depicted as a simple return to already discovered, standard truths. Once again the idea of proven standards was central. The very notion of healing is of course grounded in an idea about standard conditions of the human body and mind, postulated by the science of medicine, which the healing process seeks to restore.[61] In a similar way, the Czechoslovak reformers cast themselves as surgeons trying to restore the economy to a standard, healthy state, where ›being healthy‹ meant an automatic functioning of the market without any external interference.
As prescribed by the romantic plot, if everyone on the side of the good does his or her job, they eventually defy the odds, cure the patient and succeed: ›The market economy […] is a natural condition of mankind, and it should be possible to return to such a natural state […]. At the beginning there may be only a few [entrepreneurs], but they will be heroes, the new pioneers who will breach the dam separating us from the natural state of affairs and take others along with them […].‹[62] This was the vision presented to the Czechoslovak public by the most read Czech daily on the eve of the launch of the economic reform, bringing together the romantic plot of liberal economics – with its praise of the figure of the entrepreneur so typical of the Austrian school – with the notion of a ›return‹ to proven historical standards, which were at the same time seen to be natural and timeless, i.e. transhistorical.
In summary, we may state that while the mostly academic discussion about the market economy before 1989/90 and its large-scale implementation after this time were two different stages in Czechoslovakia, they were nevertheless fueled by common modes of representation. Introducing a specific representation of economic knowledge as a universal, objective science from some Western texts, the generation of scholars professionally socialized in the 1970s and 1980s was able to transfer this representation to the context of the local academia and to gain discursive hegemony in it. The school of scholarly thought leading to market reforms after 1989 did not emerge outside the late socialist system, but rather within its own academic structures. At the same time, it was shaped, as were other spheres of late socialist societies, by the limited availability of ›goods on the domestic market‹, in this case of scholarly economic literature. Once the constraints of political dictatorship were dismantled and the public discourse freed, this framework was filled with radical market content. The Samuelsonian pattern of argument was used as a container for a radical market agenda inspired by the Austrian model. Drawing on Samuelson’s modes of representation and the radical market approach as the represented content, the rapid liberal reforms were presented not as one of various possible paths, but more or less in the Thatcherian fashion as the only way to conform to standard expert knowledge.
(© Czech News Agency/ČTK – Photo 2015/Tomáš Turek)
The romantic plot of Austrian economic thought, which dominated the Czechoslovak community of scholarly economists, fitted very well into the changes in the revolutionary discourse immediately following the fall of communism. While the unity of the revolutionary community began to weaken during 1990, the main plot of the Austrian economic story was able to take on its dynamics. The mixture of specific representations of national history, of particular academic knowledge cast as ›standard‹, and the romantic emplotment of the economic story lying behind the particular transition concept, constructed a very tight framework. Within this framework, it was fairly easy to dismiss alternative reform proposals and thus to shape the Czechoslovak economic transformation.
In the first half of the 1990s, these representations of economic change underlined what was at the time probably the most successful liberal economic restructuring in the whole of post-communist Europe. Following the start of the distinct Slovak path of transformation after the split of Czechoslovakia in 1993, the unsuccessful attempt of Hanna Suchocka’s government to reinvigorate the halted Polish economic restructuring during the first half of the same year, and the electoral victory of the Hungarian Socialist Party in June 1994, the Czech Republic seemed to be the only remaining country in the region with a radical market agenda: it had the fastest and most extensive privatization of the economy and rapidly integrated into world markets. Thus in the mid-1990s a certain paradox emerged in East-Central Europe, whereby the Czech Republic, the country with traditionally the strongest socialist tendencies in the whole region and with a communist party – which at the end of 1989 still had probably the biggest membership/state population ratio[63] – stood as the last remaining stronghold of a radical market reform agenda. The unique popular support which the economic reforms were able to attract in Czechoslovakia and later in the Czech Republic, providing the radical reformers with two consecutive electoral victories in 1992 and 1996, suggests a complex change within the public discourse. The distinct way of casting the ongoing changes as the only possible path and one that also corresponded with the national tradition played an important part in shaping the social consensus on the economic reforms.
The aftermath of 1989/90 in East-Central and Eastern Europe brought what was probably the biggest spread of capitalism at one time in the history of this region. Never before was such a huge population caught up in capitalist economic relations in a comparably short period of time. Answers to the question of how these fast and deep changes were represented in other countries of the region might thus help us to understand the complexities of creating new, post-communist subjectivities that still form the basis of the social consensus underlying the economic and social order to this day.
Notes:
[1] The very first idea for this paper arose in preparation for the workshop ›Marketing the Market. The Representations of Economic Change in East-Central Europe 1989–1993‹ that I organized in July 2010 during my research stay at the School of History, Freiburg Institute for Advanced Studies. I wish to thank the Institute for the generous support that I had the privilege to enjoy as a one-year Fellow. Over the long time span many colleagues have commented on various versions of the paper – I wish to express my gratitude to all of them, in particular to Philipp Ther, Janos Matyás Kovács, Jacek Kochanowski, Gregor Thum, Sandra Maß, Chris Lorenz, Stefan-Ludwig Hoffmann and Vítězslav Sommer. I also wish to thank Ralf Ahrens, Marcus Böick, Marcel vom Lehn and Jan-Holger Kirsch for their valuable comments during the final revisions of the article. Finally, I wish to thank the Faculty of Social Sciences of the Charles University in Prague, which supported the research as part of its research development scheme, program P17 – Sciences of Society, Politics, and Media under the Challenge of the Times.
[2] The amount of research literature produced by scholars in the fields of economics and political and social sciences in this respect is enormous. The most important works include: Klaus von Beyme, Systemwechsel in Osteuropa, Frankfurt a.M. 1994; Anders Åslund, How Capitalism Was Built. The Transformation of Central and Eastern Europe, Russia and Central Asia, Cambridge 2007; Mitchell Oerenstein, Out of the Red. Building Capitalism and Democracy in Postcommunist Europe, Ann Arbor 2001; Dieter Segert (ed.), Postsozialismus. Hinterlassenschaften des Staatssozialismus und neue Kapitalismen in Europa, Wien 2007; David A. Dyker, Catching Up and Falling Behind. Post-Communist Transformation in Historical Perspective, London 2004; Jan Delhey, Osteuropa zwischen Marx und Markt. Soziale Ungleichheit und soziales Bewußtsein nach dem Kommunismus, Hamburg 2001; Wolfgang Merkel, Systemtransformation. Eine Einführung in die Theorie und Empirie der Transformationsforschung, Wiesbaden 2010; Wolfgang Merkel/Hans-Jürgen Puhle, Von der Diktatur zur Demokratie. Transformationen, Erfolgsbedingungen, Entwicklungspfade, Opladen 1999; Hans-Jürgen Wagener (ed.), Anpassung durch Wandel. Evolution und Transformation von Wirtschaftssystemen, Berlin 1991.
[3] Olga Pavlenko/Peter Ruggenthaler, Recent Studies on the 1989 Revolutions in Eastern Europe and on the Demise of the Soviet Union, in: Contemporary European History 24 (2015), pp. 139-150. For a conceptual discussion about the possibilities of historicizing the post-1989 era, see: Philipp Ther, Das »neue Europa« seit 1989. Überlegungen zu einer Geschichte der Transformationszeit, in: Zeithistorische Forschungen/Studies in Contemporary History 6 (2009), pp. 105-114; Padraic Kenney, The Burdens of Freedom. Eastern Europe since 1989, London 2006, pp. 16-26.
[4] See, for example: István Rév, Retroactive Justice. Prehistory of Post-Communism, Stanford 2005; Stefan Auer, Liberal Nationalism in Central Europe, London 2004; Steven Saxonberg, The Fall. A Comparative Study of the End of Communism in Czechoslovakia, East Germany, Hungary and Poland, Uppsala 2001; John Borneman, Settling Accounts. Violence, Justice and Accountability in Postsocialist Europe, Princeton 1997; Jacques Lévesque, The Enigma of 1989. The USSR and the Liberation of Eastern Europe, Berkeley 1997; Ladislav Holý, The Little Czech and the Great Czech Nation. National Identity and the Post-Communist Transformation of Society, Cambridge 1996; Roger East, Revolutions in Eastern Europe, London 1992; Timothy Garton Ash, Ein Jahrhundert wird abgewählt. Aus den Zentren Mitteleuropas 1980–1990, Munich 1990.
[5] Johanna Bockman, Markets in the Name of Socialism. The Left-Wing Origins of Neoliberalism, Stanford 2011.
[6] Michal Pullmann, Konec experimentu. Přestavba a pád komunismu v Československu [The End of an Experiment. Perestroika and the Fall of Communism in Czechoslovakia], Prague 2011; Alexei Yurchak, Everything Was Forever, Until It Was No More. The Last Soviet Generation, Princeton 2005.
[7] Gil Eyal, The Origins of Postcommunist Elites. From Prague Spring to the Breakup of Czechoslovakia, Minneapolis 2003.
[8] James Krapfl, Revolution with a Human Face. Politics, Culture and Community in Czechoslovakia 1989–1992, Ithaca 2013.
[9] Philipp Ther, Die neue Ordnung auf dem alten Kontinent. Eine Geschichte des neoliberalen Europa, Berlin 2014. For another synthetic account, see: Andreas Wirsching, Der Preis der Freiheit. Geschichte Europas in unserer Zeit, Munich 2012.
[10] Jacek Kochanowicz, Private Suffering, Public Benefit: Market Rhetoric in Poland, 1989–1993, in: East European Politics & Societies 28 (2014), pp. 103-118. On the case of Czechoslovakia, see also: Martin Dangerfield, Ideology and the Czech Transformation: Neoliberal Rhetoric or Neoliberal Reality?, in: East European Politics & Societies 11 (1997), pp. 436-469.
[11] Jiří Havel et al., Economics and System Change in Czechoslovakia, 1945–92, in: Hans-Jürgen Wagener (ed.), Economic Thought in Communist and Post-Communist Europe, London 1998, pp. 213-263, here pp. 233-241.
[12] Gil Eyal, Anti-Politics and the Spirit of Capitalism: Dissidents, Monetarists and the Czech Transition to Capitalism, in: Theory and Society 29 (2000), pp. 49-92, here pp. 72-74; Václav Klaus, Čtyři roky transformace naší ekonomiky [Four Years of our Economic Transformation], in: Politická Ekonomie 6 (1993), pp. 707-715.
[13] Václav Klaus, Zemřel poslední velikán ekonomie 20. století [The Last Great Economist of the Twentieth Century has Passed Away], in: Euro, December 21, 2009 (obituary for Samuelson).
[14] Havel et al., Economics and System Change (fn. 11), p. 256.
[15] Thomas Kuhn, The Structure of Scientific Revolutions, Chicago 1970, pp. 136-175.
[16] Arjo Klamer, The Textbook Presentation of Economic Discourse, in: Warren J. Samuels (ed.), Economics as Discourse. An Analysis of the Language of Economists, Boston 1990, pp. 129-165, here p. 133.
[17] Ibid., p. 135.
[18] Havel et al., Economics and System Change (fn. 11), pp. 236-244.
[19] Roy G.D. Allen, Mathematical Economics, London 1956; Roy G.D. Allen, Macroeconomic Theory. A Mathematical Treatment, London 1967.
[20] On the East-West entanglements of mathematical economics, see: Bockmann, Markets in the Name of Socialism (fn. 5), pp. 50-75.
[21] Ivan Boldyrev/Olessia Kirtchik, The Culture of Mathematical Economics in the Postwar Soviet Union, Working Paper of the Moscow National Research University, No. WP6/2013/05, Series WP6: Humanities, URL: <http://www.hse.ru/data/2014/01/10/1340166743/WP6_2013_05_ff.pdf>; Pekka Sutela/Vladimir Mau, Economics under Socialism: the Russian Case, in: Wagener, Economic Thought (fn. 11), pp. 33-79.
[22] See: Creating a Capitalist Czechoslovakia. An Interview with Václav Klaus, in: Tim D. Whipple (ed.), After the Velvet Revolution. Václav Havel and the New Leaders of Czechoslovakia Speak Out, New York 1991, pp. 149-156.
[23] Simon Smith, Transformation as Modernization: Readings of Post-Communist Lifeworlds, in: Simon Smith (ed.), Local Communities and Post-Communist Transformation. Czechoslovakia, the Czech Republic and Slovakia, London 2003, pp. 1-18; Pavel Machonin, K sociologii v období normalizace [Sociology in the Time of Normalization], in: Sociologický časopis [Sociological Review] 40 (2004), pp. 643-650.
[24] On the Czechoslovak forecasting scholarship, see: Vítězslav Sommer, Forecasting the Post-Socialist Future. Prognostika in the Late Socialist Czechoslovakia, 1970–1989, in: Jenny Anderson/Egle Rindzevičiute (eds), The Struggle for the Long-Term in Transnational Science and Politics. Forging the Future, New York 2015, pp. 144-168.
[25] Michal Burian, Prognostici v takzvané sametové revoluci [Forecasters in the so-called Velvet Revolution], in: Soudobé Dějiny [Contemporary History] 4 (1997), pp. 492-509, here pp. 494-496.
[26] Jiřina Šiklová, The ›Grey Zone‹ and the Future of Dissent in Czechoslovakia, in: Social Research 57 (1990), pp. 347-363.
[27] For a detailed overview of the economic debates in late-1980s Czechoslovakia, see: Jan Adam, Planning and Market in Soviet and East European Thought, 1960s – 1992, London 1993, pp. 237-246.
[28] Václav Klaus/Dušan Tříska, Ekonomické centrum, přestavba a rovnováha [Economic Center, Restructuring and Equilibrium], in: Politická Ekonomie [Political Economy] 36 (1988), pp. 817-829.
[29] Ibid., p. 817.
[30] Ibid., p. 818.
[31] Ibid.
[32] See: Katherine Verdery, What Was Socialism and What Comes Next?, Princeton 1996, pp. 19-35.
[33] Klaus/Tříska, Ekonomické centrum (fn. 28), p. 825.
[34] Ibid., p. 824.
[35] See the seminal work: Hayden White, Tropics of Discourse. Essays in Cultural Criticism, Baltimore 1978, in particular pp. 51-80.
[36] Arjo Klamer, Speaking of Economics. How to get in the Conversation, London 2007, p. 116; Deirdre N. McCloskey, The Rhetoric of Economics, Brighton 1986, 2nd ed. Madison 1998, pp. 20-51; Deirdre N. McCloskey, Knowledge and Persuasion in Economics, Cambridge 1994, pp. 25-52.
[37] Krapfl, Revolution with a Human Face (fn. 8), pp. 11-34.
[38] James Krapfl, Revolution and Revolt against Revolution: Czechoslovakia 1989, in: Kevin McDermott/Matthew Stibbe (eds), Revolution and Resistance in Eastern Europe. Challenges to Communist Rule, Oxford 2006, pp. 175-193.
[39] Jiří Suk, Vznik Občanského Fóra a proměny jeho struktury (19. listopad až 10. prosinec 1989) [The Formation of the Civic Forum and the Transformation of its Structure (November 19 – December 10, 1989], in: Soudobé Dějiny [Contemporary History] 2 (1995), pp. 17-41.
[40] Eyal, Anti-Politics and the Spirit of Capitalism (fn. 12), p. 72; Burian, Prognostici (fn. 25), pp. 499-501.
[41] For a detailed analysis of the ways in which this particular concept gained dominance within the governmental bodies, see: Jiří Suk, Labyrintem Revoluce. Aktéři, zápletky a křižovatky jedné politické krize (od listopadu 1989 do června 1990) [The Labyrinth of Revolution. Actors, Episodes and Crossroads of one Political Crisis (November 1989 – June 1990)], Praha 2003, pp. 400-414. For the broader context of the rise and spread of the neoliberal agenda, see: Philip Mirowski/Dieter Plehwe (eds), The Road from Mont Pèlerin. The Making of the Neoliberal Thought Collective, Cambridge 2009.
[42] Odborníci z prognostického ústavu ČSAV uvažují [Experts from Forecasting Institute of the Czechoslovak Academy of Sciences Consider], in: Mladá Fronta Dnes [Young Front Today], December 2, 1989, p. 3; Petr Uhl, The Fight for Socialist Democracy in Czechoslovakia, in: New Left Review 179 (January – February 1990), pp. 11-19, here p. 13.
[43] Scénář ekonomické reformy [Scenario for Economic Reform], in: Hospodářské noviny [Business Daily], September 4, 1990.
[44] Similar comments can be found all over the media in the second half of 1990. This particular quote stems from a radio interview with Václav Klaus conducted in September 1990. Published in: Václav Klaus, O tvář zítřka [About the Face of Tomorrow], Praha 1991, p. 100.
[45] As a main tool for controlling wage growth, high penalties were prescribed for enterprises where wages rose by more than 5 percent. Adam, Planning and Market (fn. 27), p. 248.
[46] Martin Myant, The Rise and Fall of Czech Capitalism. Economic Development in the Czech Republic since 1989, Cheltenham 2003, pp. 25-31.
[47] Herbert Kitschelt, Formation of Party Cleavages in Post-Communist Democracies, in: Party Politics 1 (1995), pp. 447-472.
[48] On the main ›revolutionary ideals‹ of the Czechoslovak anti-communist upheaval, see: Krapfl, Revolution with a Human Face (fn. 8), pp. 74-110.
[49] Myant, The Rise and Fall of Czech Capitalism (fn. 46), p. 14.
[50] Kieran Williams, National Myths in the New Czech Liberalism, in: Geoffrey Hoskin/George Schöpflin (eds), Myths and Nationhood, London 1997, pp. 132-140, here p. 133.
[51] O penězích. Rozhovor s ministrem financí Václavem Klausem [About Money. Interview with the finance minister Václav Klaus], in: Mladá Fronta Dnes [Young Front Today], October 6, 1990, p. 2.
[52] Václav Klaus, Síla idejí [The Power of Ideas], in: Literární noviny [Literary Review], April 25, 1991, p. 2.
[53] For various reform blueprints, see: Vittorio Corbo/Fabrizio Coricelli/Jan Bossak (eds), Reforming Central and Eastern European Economies. A World Bank Symposium, Washington 1991; Jeffrey Sachs, Poland and Eastern Europe: What is to be Done?, in: Andras Koves/Paul Marer (eds), Foreign Economics Liberalization, Westview 1991, pp. 235-246; Peter Murrell, Evolutionary and Radical Approaches to Economic Reform, in: Kazimierz Z. Poznanski (ed.), Stabilization and Privatization in Poland. An Economic Evaluation of the Shock Therapy Program, Boston 1993, pp. 215-231; Václav Klusoň/Lubomír Mlčoch/Otakar Turek, Přestavba hospodářského mechanismu. Deskripce tradičního modelu, východiska řešení a hospodářská politika přechodu [Transformation of the Economic Mechanism. Description of Traditional Model, Possibilities of Solution and Economic Transformation Policy], Praha 1990; Valtr Komárek, Prognóza a program [Prognosis and Program], Praha 1990; Karel Dyba/Jan Švejnar, Stabilization and Transition in Czechoslovakia, Prague 1992; Václav Klaus, Signale aus dem Herzen Europas. Ausgewählte Beiträge zur Gesellschafts- und Wirtschaftspolitik nach der Wende in der Tschechoslowakei, Wiesbaden 1991; Václav Klaus, Dismantling Socialism. A Preliminary Report, Auckland 1991.
[54] Sean Heanley, The New Right in the New Europe. Czech Transformation and Right-wing Politics, 1989–2006, London 2008, pp. 15-16.
[55] Mladá Fronta Dnes [Young Front Today], December 8, 1990, p. 1.
[56] Mladá Fronta Dnes [Young Front Today], September 10, 1990, pp. 1-2.
[57] Mladá Fronta Dnes [Young Front Today], October 8, 1990, pp. 1-2.
[58] Mladá Fronta Dnes [Young Front Today], January 31, 1991, p. 3.
[59] Tomáš Sniegoň, Looking Back, Going Forward. Czech and Slovak Dominant Historical Narratives of the ›long 1990s‹, in: Barbara Tornquist-Plewa/Krzysztof Stala (eds), Cultural Transformations After Communism. Central and Eastern Europe in Focus, Lund 2011, pp. 180-213.
[60] The body of economic literature on Czechoslovak privatization is enormous. See, for example: Jan Hanousek/Evžen Kočenda, The Impact of Czech Mass Privatization on Corporate Governance, in: Journal of Economic Studies 30 (2003), pp. 278-293; Jan Mládek/Jiří Švejnar, Is Czech Voucher Privatization a Success?, in: Transitions 4 (1997), pp. 92-95; Miroslav Singer/Jiří Švejnar, Using Vouchers to Privatize an Economy: The Czech and Slovak Case, in: Economics of Transition 2 (1994), pp. 43-69.
[61] On body and medical metaphors and economics, see particularly: Frank Boers, ›No Pain, No Gain‹ in a Free Market Rhetoric: A Test for Cognitive Semantics?, in: Metaphor and Symbol 12 (1997), pp. 231-241. Further, see: Philipp Sarasin, Infizierte Körper, kontaminierte Sprachen. Metaphern als Gegenstand der Wissenschaftsgeschichte, in: Philipp Sarasin, Geschichtswissenschaft und Diskursanalyse, Frankfurt a.M. 2003, pp. 191-230.
[62] Rána pobloudilým marxistům. Rozhovor s poradcem pro privatizaci Dušanem Třískou [A blow to bewildered Marxists. Interview with the privatization advisor Dušan Tříska], in: Mladá Fronta Dnes [Young Front Today], September 12, 1990, p. 3.
[63] In December 1989, the Czechoslovak Communist Party still had about 1.7 million members. With an overall Czechoslovak population of about 15 million people, it encompassed approximately 12 percent of the whole population. François Mayer, Češi a jejich komunismus. Paměť a politická identita [The Czechs and Their Communism. Memory and Political Identity], Prague 2009, p. 58.